Values of n where α(n) = n (up to 10000):
[1, 5, 12, 25, 60, 125, 300, 625, 1500, 3125, 7500]Self-Fibonacci Numbers
Here’s a seemingly simple question that lacks a clean solution:
For what positive integers \(n\) does \(n\) divide \(F_n\), where \(F_n\) denotes the \(n^{\text{th}}\) Fibonacci number?
According to the On-Line Encyclopedia of Integer Sequences (OEIS), such numbers are called “Self-Fibonacci numbers”: https://oeis.org/A023172. The sequence begins:
1, 5, 12, 24, 25, 36, 48, 60, 72, 96, 108, 120, 125, 144, 168, 180, 192, 216, 240, 288, 300, 324, 336, 360, 384, 432, 480, 504, 540, 552, 576, 600, 612, 625, 648, 660, 672, 684, 720, 768, 840, 864, 900, 960, 972, 1008, 1080, 1104, 1152, 1176, 1200, 1224, 1296, 1320
One approach to this question is as follows:
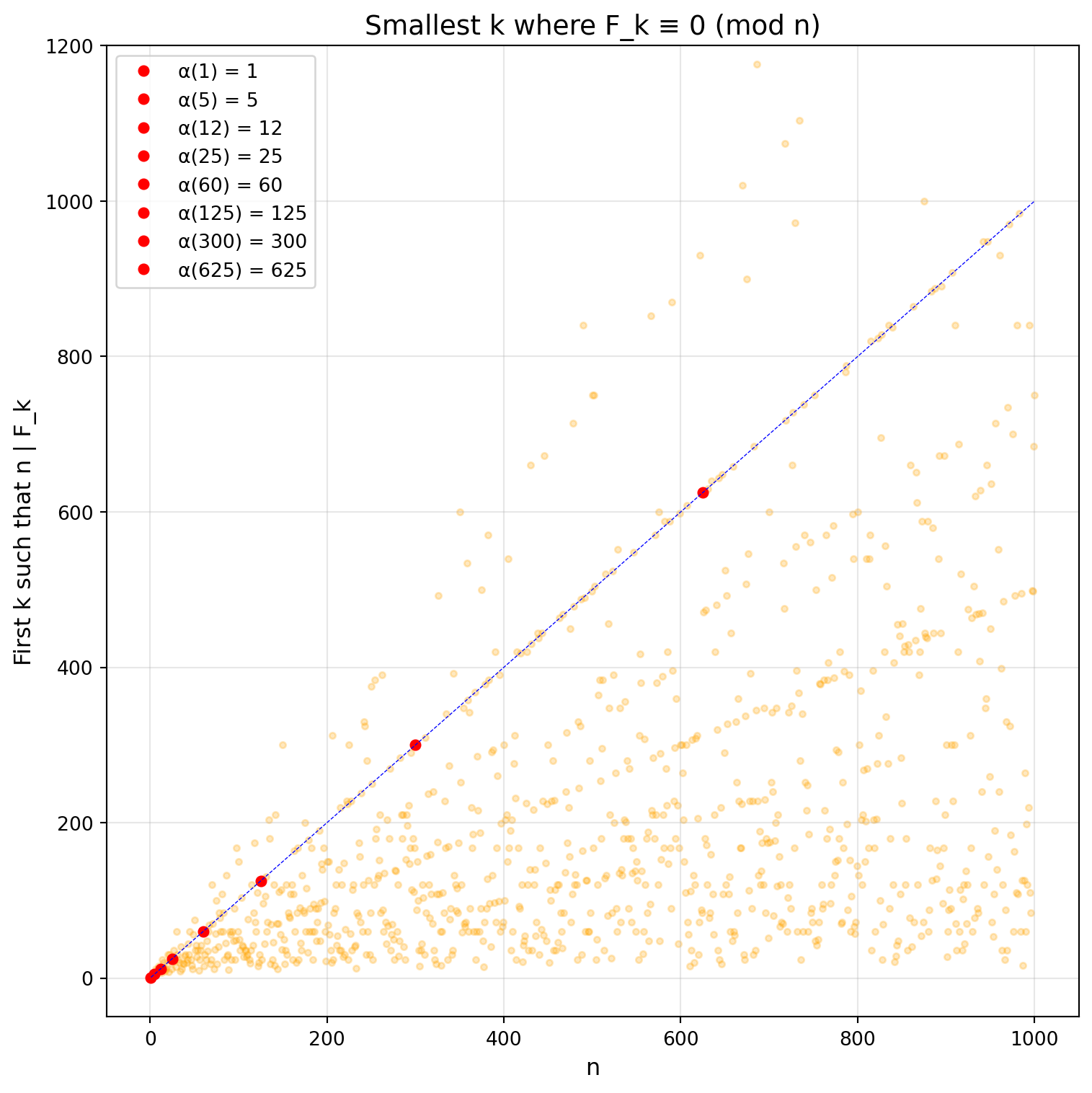
Let \(\alpha(n)\) be the smallest positive integer \(k\) such that \(n \mid F_k\). Note that if \(n \mid F_k\), then \(n \mid F_{mk}\) for all positive integers \(m\). Therefore, the self-Fibonacci numbers are exactly those for which \(\alpha(n) \mid n\).
This sequence is fascinating, with apparently no simple formula! I explored the following related question:
For what positive integers \(n\) does \(\alpha(n) = n\)?
Here’s the list of such numbers up to 10,000.
This is a much simpler question, and the sequence appears to consist of all numbers that are powers of 5 or 12 times a power of 5. The OEIS entry for this sequence is https://oeis.org/A289586.
The only integers \(n\) such that \(\alpha(n) = n\) are of the form \(5^k\) or \(12 \cdot 5^k\) for some non-negative integer \(k\).
I’m not certain this is true, but it holds for all integers up to 10,000. I’m also interested in understanding the distribution of \(n / \alpha(n)\). When plotting \(n / \alpha(n)\), most values fall above 1, though some are less than or equal to 1.
Below is a table of \(n / \alpha(n)\) for all integers \(n\) up to 10,000. Surprisingly, the most common value is not 1 but \(4/3\).
I wonder what patterns exist in the ratios \(n / \alpha(n)\)…
What is the distribution of the ratios \(n / \alpha(n)\)?
For every integer \(k\), is there some integer \(n\) such that \(n / \alpha(n) = k\)?
Can we exploit the fact that
\[ F_k = \dfrac{1}{\sqrt{5}} \left( \phi^k - \psi^k \right) \]
where \(\phi = \frac{1 + \sqrt{5}}{2}\) and \(\psi = \frac{1 - \sqrt{5}}{2}\), to find a closed form for \(\alpha(n)\)? We know that \(\mathbb{Z}[\phi]\) is a Euclidean domain so we can have access to number theoretic tools such as divisibility and the Euclidean algorithm.

| n / α(n) | count | n values |
|-----------:|--------:|:--------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1.33333 | 31 | 8, 16, 32, 40, 64, 80, 128, 160, 200, 256, 320, 400, 512, 640, 800, 1000, 1024, 1280, 1600, 2000, 2048, 2560, 3200, 4000, 4096, 5000, 5120, 6400, 8000, 8192, 10000 |
| 2.625 | 29 | 21, 63, 105, 147, 189, 315, 441, 525, 567, 735, 945, 1029, 1323, 1575, 1701, 2205, 2625, 2835, 3087, 3675, 3969, 4725, 5103, 5145, 6615, 7203, 7875, 8505, 9261 |
| 12 | 27 | 144, 288, 432, 576, 720, 864, 1152, 1296, 1440, 1728, 2160, 2304, 2592, 2880, 3456, 3600, 3888, 4320, 4608, 5184, 5760, 6480, 6912, 7200, 7776, 8640, 9216 |
| 0.75 | 25 | 3, 9, 15, 27, 45, 75, 81, 135, 225, 243, 375, 405, 675, 729, 1125, 1215, 1875, 2025, 2187, 3375, 3645, 5625, 6075, 6561, 9375 |
| 1.39286 | 20 | 39, 117, 195, 351, 507, 585, 975, 1053, 1521, 1755, 2535, 2925, 3159, 4563, 4875, 5265, 6591, 7605, 8775, 9477 |
| 4 | 19 | 48, 96, 192, 240, 384, 480, 768, 960, 1200, 1536, 1920, 2400, 3072, 3840, 4800, 6000, 6144, 7680, 9600 |
| 2.47619 | 18 | 104, 208, 416, 520, 832, 1040, 1352, 1664, 2080, 2600, 2704, 3328, 4160, 5200, 5408, 6656, 6760, 8320 |
| 1.5 | 16 | 18, 54, 90, 162, 270, 450, 486, 810, 1350, 1458, 2250, 2430, 4050, 4374, 6750, 7290 |
| 7.55556 | 16 | 136, 272, 544, 680, 1088, 1360, 2176, 2312, 2720, 3400, 4352, 4624, 5440, 6800, 8704, 9248 |
| 9.33333 | 15 | 224, 448, 896, 1120, 1568, 1792, 2240, 3136, 3584, 4480, 5600, 6272, 7168, 7840, 8960 |
| 8.44444 | 15 | 152, 304, 608, 760, 1216, 1520, 2432, 2888, 3040, 3800, 4864, 5776, 6080, 7600, 9728 |
| 1.2381 | 15 | 26, 52, 130, 260, 338, 650, 676, 1300, 1690, 3250, 3380, 4394, 6500, 8450, 8788 |
| 5.25 | 14 | 126, 378, 630, 882, 1134, 1890, 2646, 3150, 3402, 4410, 5670, 6174, 7938, 9450 |
| 3 | 14 | 36, 108, 180, 324, 540, 900, 972, 1620, 2700, 2916, 4500, 4860, 8100, 8748 |
| 1.85714 | 13 | 13, 65, 156, 169, 325, 780, 845, 1625, 2028, 2197, 3900, 4225, 8125 |
| 3.77778 | 13 | 34, 68, 170, 340, 578, 850, 1156, 1700, 2890, 4250, 5780, 8500, 9826 |
| 0.875 | 13 | 7, 35, 49, 175, 245, 343, 875, 1225, 1715, 2401, 4375, 6125, 8575 |
| 3.10714 | 12 | 87, 261, 435, 783, 1305, 2175, 2349, 2523, 3915, 6525, 7047, 7569 |
| 6 | 12 | 72, 216, 360, 648, 1080, 1800, 1944, 3240, 5400, 5832, 9000, 9720 |
| 5.52381 | 12 | 232, 464, 928, 1160, 1856, 2320, 3712, 4640, 5800, 6728, 7424, 9280 |
| 2.93333 | 11 | 88, 176, 352, 704, 968, 1408, 1936, 2816, 3872, 5632, 7744 |
| 5.5 | 11 | 55, 275, 330, 605, 1375, 1650, 3025, 3630, 6655, 6875, 8250 |
| 8.25 | 11 | 165, 495, 825, 1485, 1815, 2475, 4125, 4455, 5445, 7425, 9075 |
| 1.46053 | 11 | 111, 333, 555, 999, 1665, 2775, 2997, 4107, 4995, 8325, 8991 |
| 1 | 11 | 1, 5, 12, 25, 60, 125, 300, 625, 1500, 3125, 7500 |
| 0.583333 | 11 | 14, 70, 98, 350, 490, 686, 1750, 2450, 3430, 4802, 8750 |
| 1.65 | 11 | 33, 99, 297, 363, 891, 1089, 2673, 3267, 3993, 8019, 9801 |
| 0.666667 | 11 | 2, 4, 10, 20, 50, 100, 250, 500, 1250, 2500, 6250 |
| 10.5 | 10 | 252, 756, 1260, 1764, 2268, 3780, 5292, 6300, 6804, 8820 |
| 1.16667 | 10 | 28, 140, 196, 700, 980, 1372, 3500, 4900, 6860, 9604 |