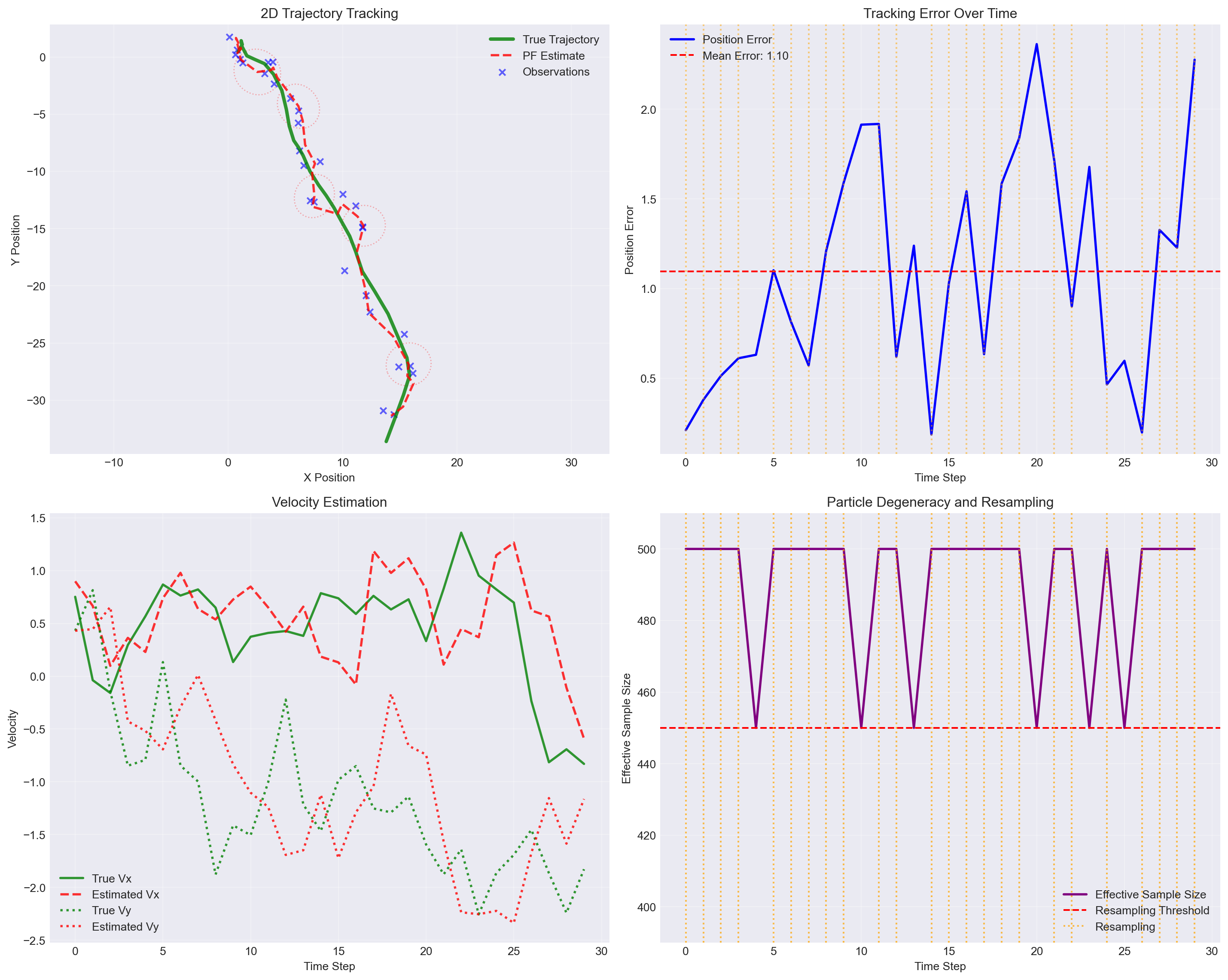
Particle Filter Performance:
Number of particles: 500
Final position error: 2.276
Mean position error: 1.097
Resampling frequency: 24/30 time steps18 Particle Filters
18.1 Introduction
Particle filtering, also known as Sequential Monte Carlo (SMC) or Sequential Importance Sampling, is a powerful computational method for performing inference in dynamic systems where we have:
- Sequential observations arriving over time
- Hidden state variables that evolve according to some dynamics
- Nonlinear or non-Gaussian relationships that make analytical solutions intractable
Consider a hidden Markov model where we observe a sequence \(\mathbf{y}_{1:T} = \{\mathbf{y}_1, \mathbf{y}_2, \ldots, \mathbf{y}_T\}\) and want to infer the hidden states \(\mathbf{x}_{1:T} = \{\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_T\}\). The system is characterized by:
- State transition model: \(p(\mathbf{x}_t | \mathbf{x}_{t-1})\) - how the hidden state evolves
- Observation model: \(p(\mathbf{y}_t | \mathbf{x}_t)\) - how observations relate to hidden states
- Initial state distribution: \(p(\mathbf{x}_0)\)
Our goal is to compute the filtering distribution \(p(\mathbf{x}_t | \mathbf{y}_{1:t})\), which represents our belief about the current state given all observations up to time \(t\).
18.1.1 The Challenge
For linear-Gaussian systems, the Kalman filter provides an exact analytical solution. However, for nonlinear or non-Gaussian systems, the filtering distribution cannot be computed analytically. The key challenges are:
- Intractable integrals: Computing \(p(\mathbf{x}_t | \mathbf{y}_{1:t})\) requires high-dimensional integration
- Sequential nature: We need real-time updates as new observations arrive
- Curse of dimensionality: Grid-based methods become infeasible in high dimensions
18.1.2 The Particle Filter Solution
Particle filters address these challenges by representing the filtering distribution using a set of particles (samples) with associated weights:
\[ p(\mathbf{x}_t | \mathbf{y}_{1:t}) \approx \sum_{i=1}^{N} w_t^{(i)} \delta(\mathbf{x}_t - \mathbf{x}_t^{(i)}), \]
where:
- \(\{\mathbf{x}_t^{(i)}\}_{i=1}^{N}\) are particles representing possible states
- \(\{w_t^{(i)}\}_{i=1}^{N}\) are normalized weights such that \(\sum_{i=1}^{N} w_t^{(i)} = 1\)
- \(\delta(\cdot)\) is the Dirac delta function
This Monte Carlo approximation allows us to:
- Handle arbitrary nonlinearities and noise distributions
- Update beliefs sequentially as new data arrives
- Compute expectations: \(\mathbb{E}[f(\mathbf{x}_t) | \mathbf{y}_{1:t}] \approx \sum_{i=1}^{N} w_t^{(i)} f(\mathbf{x}_t^{(i)})\)
Note
Key Insight: Particle filters extend importance sampling to sequential settings, where we maintain and update a particle approximation over time rather than drawing fresh samples for each time step.
18.1.3 Applications
Particle filters are widely used in:
- Object tracking in computer vision
- Robot localization and SLAM (Simultaneous Localization and Mapping)
- Financial modeling with stochastic volatility
- Signal processing and communications
- Epidemiological modeling and disease spread
- Weather forecasting and climate modeling
The flexibility to handle complex, nonlinear dynamics makes particle filters indispensable when Kalman filters fail.
18.3 Particle Filtering Algorithm
18.3.1 The Bootstrap Filter - The Simple Case
The most intuitive approach is the bootstrap filter. Here, we generate new particles by simply following the natural dynamics of the system (the state evolution model), then update weights based on how well each particle explains the new observation.
Bootstrap Weight Update: \[ \boxed{\tilde{w}_t^{(i)} \propto w_{t-1}^{(i)} \cdot p(\mathbf{y}_t | \mathbf{x}_t^{(i)})} \]
What this means:
- \(w_{t-1}^{(i)}\): Previous weight of particle \(i\)
- \(p(\mathbf{y}_t | \mathbf{x}_t^{(i)})\): Likelihood - How well particle \(i\) explains the new observation
- Particles that better match the observation get higher weights
- We normalize so all weights sum to 1: \(w_t^{(i)} = \tilde{w}_t^{(i)} / \sum_{j=1}^N \tilde{w}_t^{(j)}\)
Why This Works: We’re essentially asking “given what we observed, which particles were in the right place?” Particles that predicted something close to the actual observation become more important.
18.3.2 General Formula - Correcting for Different Proposals
Sometimes we want to be smarter about where we place new particles instead of just following the natural dynamics. We might use a proposal distribution \(q(\mathbf{x}_t^{(i)} | \cdot)\) that incorporates the current observation to guide particles toward more promising regions.
Why Use a Different Proposal?
- Bootstrap problem: If the observation is very informative but the system dynamics are very noisy, most particles following natural dynamics will end up far from where the observation suggests they should be.
- Efficiency: We waste computational effort on particles that will get very low weights.
- Better exploration: A good proposal can guide particles toward regions that are both dynamically plausible AND consistent with the observation.
- Computational efficiency: It might be computationally expensive to evolve many particles according to the state evolution model.
Example: If you are tracking an object in the 2D plane that usually moves slowly, but you suddenly observe it far from where you expected. The bootstrap filter would propose particles near the previous location (following slow dynamics), but they’d all get low weights. A smarter proposal would generate particles closer to where the observation suggests the object actually is.
When we do this, we need to correct our weights using importance sampling:
\[ \boxed{\tilde{w}_t^{(i)} \propto w_{t-1}^{(i)} \cdot p(\mathbf{y}_t | \mathbf{x}_t^{(i)}) \cdot \frac{ p(\mathbf{x}_t^{(i)} | \mathbf{x}_{t-1}^{(i)})}{q(\mathbf{x}_t^{(i)} | \mathbf{x}_{0:t-1}^{(i)}, \mathbf{y}_{1:t})}} \]
What the correction does:
- \(p(\mathbf{x}_t^{(i)} | \mathbf{x}_{t-1}^{(i)})\): Transition probability - How likely this particle movement is under the true dynamics
- \(q(\mathbf{x}_t^{(i)} | \cdot)\): Proposal probability - How likely this particle movement is under our artificial proposal
- The ratio \(\frac{p(\cdot)}{q(\cdot)}\) corrects for the bias introduced by not sampling from the natural dynamics
Intuition: If we artificially push particles toward certain regions (high \(q\)), we need to down-weight them proportionally. If we place particles in regions that are naturally likely (high \(p\)), we up-weight them.
The bootstrap filter is the special case where \(q(\mathbf{x}_t^{(i)} | \cdot) = p(\mathbf{x}_t^{(i)} | \mathbf{x}_{t-1}^{(i)})\), so the transition probabilities cancel out and we get the simpler formula.
18.3.3 Effective Sample Size and Resampling
The effective sample size \(N_{\text{eff}} = 1/\sum_{i=1}^N (w_t^{(i)})^2\) measures particle diversity, with \(N_{\text{eff}} = 1\) indicating complete degeneracy (one particle has weight 1) and \(N_{\text{eff}} = N\) indicating uniform weights.
Connection to Variance: The effective sample size is inversely related to the variance of the weight distribution. For a discrete probability mass function with weights \(\{w^{(i)}\}\), the variance is:
\[\text{Var}(w) = \sum_{i=1}^N (w^{(i)})^2 - \left(\sum_{i=1}^N w^{(i)}\right)^2\]
Since the weights are normalized (\(\sum_{i=1}^N w^{(i)} = 1\)), this becomes:
\[\text{Var}(w) = \sum_{i=1}^N (w^{(i)})^2 - 1\]
Therefore: \(\sum_{i=1}^N (w^{(i)})^2 = \text{Var}(w) + 1\)
This shows that \(N_{\text{eff}} = \frac{1}{\text{Var}(w) + 1}\), meaning:
- High variance in weights → Low \(N_{\text{eff}}\) → Few effective particles
- Low variance in weights → High \(N_{\text{eff}}\) → Many effective particles
When weights are highly unequal (high variance), most particles contribute little to the approximation, reducing the effective sample size. When weights are nearly uniform (low variance), all particles contribute meaningfully.
Resampling fixes the weight imbalance by creating a new set of particles \(\{\tilde{\mathbf{x}}_t^{(i)}\}_{i=1}^N\). We randomly select particles based on their weights - particles with higher weights get picked more often, while particles with low weights may be discarded.
We draw \(N\) new particles from the current set, where each particle’s chance of being selected equals its weight. A particle with weight 0.4 has a 40% chance of being chosen on each draw. After resampling all particles get equal weight \(w_t^{(i)} = 1/N\) since they now represent an unweighted sample from our belief distribution.
Resampling solves the weight problem (restores \(N_{\text{eff}} = N\)) but introduces randomness. Sometimes good particles are lost by bad luck, and we end up with multiple copies of the same particle, reducing diversity.
Bootstrap Particle Filter Algorithm
Input: \(\{\mathbf{x}_0^{(i)}, w_0^{(i)} = 1/N\}_{i=1}^N\), observations \(\mathbf{y}_{1:T}\)
For \(t = 1, \ldots, T\):
- Predict: For \(i = 1, \ldots, N\): \(\mathbf{x}_t^{(i)} \sim p(\mathbf{x}_t | \mathbf{x}_{t-1}^{(i)})\)
- Weight: For \(i = 1, \ldots, N\): \(\tilde{w}_t^{(i)} = w_{t-1}^{(i)} \cdot p(\mathbf{y}_t | \mathbf{x}_t^{(i)})\)
- Normalize: For \(i = 1, \ldots, N\): \(w_t^{(i)} = \tilde{w}_t^{(i)} / \sum_{j=1}^N \tilde{w}_t^{(j)}\)
- Resample: If \(N_{\text{eff}} = 1/\sum_{i=1}^N (w_t^{(i)})^2 < N_{\text{threshold}}\):
- Draw \(\{\tilde{\mathbf{x}}_t^{(i)}\}_{i=1}^N\) from \(\{\mathbf{x}_t^{(i)}\}_{i=1}^N\) with probabilities \(\{w_t^{(i)}\}_{i=1}^N\)
- Set \(\mathbf{x}_t^{(i)} = \tilde{\mathbf{x}}_t^{(i)}\) and \(w_t^{(i)} = 1/N\) for all \(i\)
Output: \(p(\mathbf{x}_t | \mathbf{y}_{1:t}) \approx \sum_{i=1}^N w_t^{(i)} \delta(\mathbf{x}_t - \mathbf{x}_t^{(i)})\)
18.3.4 Particle Filtering for 2D Object Tracking
Weight Update Derivation: For the bootstrap proposal \(q(\mathbf{x}_t | \mathbf{x}_{t-1}, \mathbf{y}_{1:t}) = p(\mathbf{x}_t | \mathbf{x}_{t-1})\), the weight update simplifies to:
\[ \tilde{w}_t^{(i)} = w_{t-1}^{(i)} \cdot p(\mathbf{y}_t | \mathbf{x}_t^{(i)}) \]
For the tracking model, the likelihood is:
\[ p(\mathbf{y}_t | \mathbf{x}_t^{(i)}) = \mathcal{N}(\mathbf{y}_t; \mathbf{H} \mathbf{x}_t^{(i)}, \mathbf{R}) \]
where \(\mathbf{H} \mathbf{x}_t^{(i)} = [p_x^{(i)}, p_y^{(i)}]^{\top}\) extracts the position components from the state vector \(\mathbf{x}_t^{(i)} = [p_x^{(i)}, p_y^{(i)}, v_x^{(i)}, v_y^{(i)}]^{\top}\). The observation residual is:
\[ \mathbf{r}_t^{(i)} = \mathbf{y}_t - \mathbf{H} \mathbf{x}_t^{(i)} = \begin{pmatrix} y_{x,t} - p_x^{(i)} \\ y_{y,t} - p_y^{(i)} \end{pmatrix} \]
Therefore, the weight update becomes:
\[ \tilde{w}_t^{(i)} = w_{t-1}^{(i)} \cdot \mathcal{N}(\mathbf{y}_t; \mathbf{H} \mathbf{x}_t^{(i)}, \mathbf{R}) = w_{t-1}^{(i)} \cdot \frac{1}{\sqrt{(2\pi)^2 |\mathbf{R}|}} \exp\left(-\frac{1}{2} (\mathbf{r}_t^{(i)})^{\top} \mathbf{R}^{-1} \mathbf{r}_t^{(i)}\right) \]
Bootstrap Particle Filter Algorithm for Object Tracking:
Input: \(\{\mathbf{x}_0^{(i)}, w_0^{(i)} = 1/N\}_{i=1}^N\), observations \(\mathbf{y}_{1:T}\)
For \(t = 1, \ldots, T\):
Predict: For \(i = 1, \ldots, N\): \[\mathbf{x}_t^{(i)} = \mathbf{F} \mathbf{x}_{t-1}^{(i)} + \boldsymbol{\epsilon}_t^{(i)}, \quad \boldsymbol{\epsilon}_t^{(i)} \sim \mathcal{N}(\mathbf{0}, \mathbf{Q})\]
Weight: For \(i = 1, \ldots, N\): \[\tilde{w}_t^{(i)} = w_{t-1}^{(i)} \cdot \mathcal{N}(\mathbf{y}_t; \mathbf{H} \mathbf{x}_t^{(i)}, \mathbf{R})\]
Normalize: For \(i = 1, \ldots, N\): \[w_t^{(i)} = \frac{\tilde{w}_t^{(i)}}{\sum_{j=1}^N \tilde{w}_t^{(j)}}\]
Estimate: \[\hat{\mathbf{x}}_t = \sum_{i=1}^N w_t^{(i)} \mathbf{x}_t^{(i)}\]
Resample: If \(N_{\text{eff}} = 1/\sum_{i=1}^N (w_t^{(i)})^2 < N_{\text{threshold}}\):
- Draw \(\{\tilde{\mathbf{x}}_t^{(i)}\}_{i=1}^N\) from \(\{\mathbf{x}_t^{(i)}\}_{i=1}^N\) with probabilities \(\{w_t^{(i)}\}_{i=1}^N\)
- Set \(\mathbf{x}_t^{(i)} = \tilde{\mathbf{x}}_t^{(i)}\) and \(w_t^{(i)} = 1/N\) for all \(i\)
Output: Position estimate \(\hat{\mathbf{p}}_t = [\hat{p}_{x,t}, \hat{p}_{y,t}]^{\top}\) and velocity estimate \(\hat{\mathbf{v}}_t = [\hat{v}_{x,t}, \hat{v}_{y,t}]^{\top}\)
18.4 Particle Filter Implementation
The following implementation demonstrates a complete particle filter for 2D object tracking. The demonstration tracks an object moving in 2D space with:
- Process noise: Models random accelerations (\(\sigma_a = 0.5\))
- Observation noise: GPS-like position measurements (\(\sigma_r = 1.0\))
- Particles: 500 particles provide good approximation quality
- Duration: 30 time steps with unit time intervals
The visualization shows the particle filter’s ability to track the true trajectory despite noisy observations, with automatic resampling maintaining particle diversity throughout the simulation.
18.5 Conclusion
Particle filters provide a powerful and flexible framework for tracking hidden states in complex dynamic systems. Unlike the Kalman filter, which requires linear dynamics and Gaussian noise, particle filters can handle arbitrary nonlinearities and any noise distribution by representing beliefs as a cloud of weighted samples.
18.5.1 Key Strengths
- Flexibility: Works with any state evolution and observation model.
- Intuitive: The particle representation mirrors how we naturally think about uncertainty.
- Scalable: Performance degrades gracefully as system complexity increases.
- Real-time capable: Sequential updates make it suitable for online applications.
18.5.2 Limitations and Challenges
- Computational cost: Requires many particles for good approximation, especially in high dimensions.
- Sample impoverishment: Resampling can reduce particle diversity over time.
- Curse of dimensionality: Performance degrades exponentially with state dimension.
- Tuning required: Number of particles and resampling thresholds need careful selection.
18.5.3 When to Use Particle Filters
Particle filters excel when:
- The system is nonlinear or has non-Gaussian noise.
- You need real-time state estimation.
- The state space is moderate dimensional (typically < 10-20 dimensions).
- Computational resources are available for running many particles.
Consider alternatives when:
- The system is linear-Gaussian (use Kalman filter).
- The state space is very high-dimensional (consider ensemble methods).
- Computational resources are severely limited.