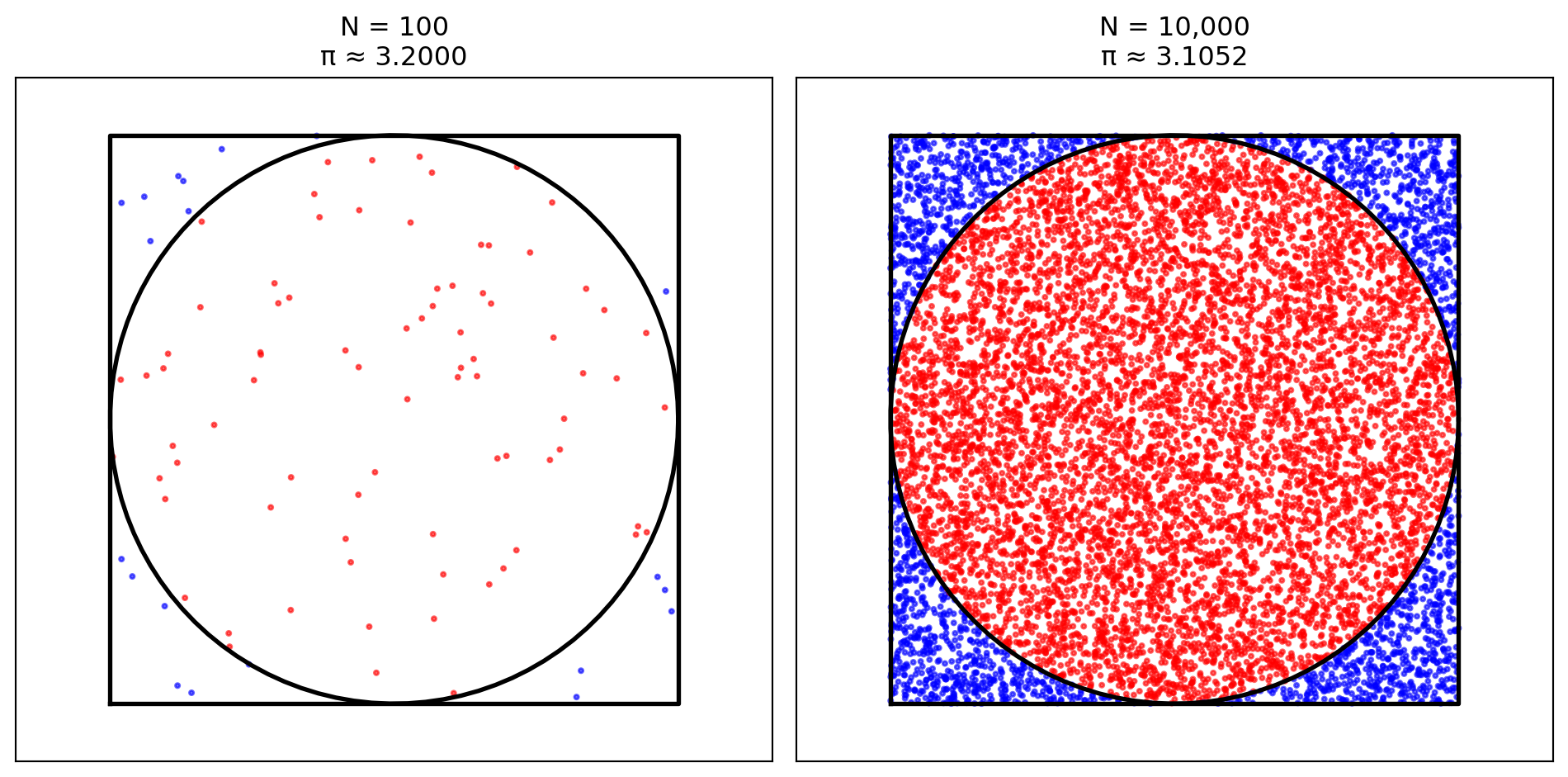
Monte Carlo π Estimation Results
==================================================
Sample Size Points Inside π Estimate Absolute Error Standard Error
100 80 3.2000 0.0584 0.1600
10,000 7,763 3.1052 0.0364 0.0167We begin with a classic Monte Carlo application: estimating the value of \(\pi\) using geometric probability. This example illustrates the core principles of Monte Carlo simulation while providing an intuitive geometric interpretation.
Consider a unit circle inscribed in a square with side length 2, both centered at the origin. The circle has radius \(r = 1\) and area \(A_{\text{circle}} = \pi\), while the square has area \(A_{\text{square}} = 4\). The ratio of these areas is \(\pi/4\).
If we randomly sample points uniformly within the square, the probability that any point falls inside the inscribed circle equals this area ratio. This geometric probability provides our pathway to estimating \(\pi\).
To formulate this as a Monte Carlo problem, let \((X, Y)\) be uniformly distributed on \([-1, 1] \times [-1, 1]\) and define the indicator random variable: \[I(X, Y) = \mathbf{1}_{\{X^2 + Y^2 \leq 1\}} = \begin{cases} 1 & \text{if } X^2 + Y^2 \leq 1 \text{ (inside circle)} \\ 0 & \text{if } X^2 + Y^2 > 1 \text{ (outside circle)} \end{cases}\]
The expected value of this indicator function gives us the desired probability: \[\mathbb{E}[I(X, Y)] = P(X^2 + Y^2 \leq 1) = \frac{\text{Area of unit circle}}{\text{Area of square}} = \frac{\pi}{4}\]
Therefore \(\pi = 4\mathbb{E}[I(X, Y)]\), and given \(N\) independent samples \((X_1, Y_1), \ldots, (X_N, Y_N)\), our Monte Carlo estimator is: \[\hat{\pi}_N = 4 \cdot \frac{1}{N}\sum_{i=1}^{N} I(X_i, Y_i) = \frac{4 \cdot \text{(number of points inside circle)}}{N}\]
This estimator possesses several important statistical properties. First, it is unbiased: \[\mathbb{E}[\hat{\pi}_N] = 4\mathbb{E}\left[\frac{1}{N}\sum_{i=1}^{N} I_i\right] = 4\mathbb{E}[I] = 4 \cdot \frac{\pi}{4} = \pi\]
Since \(I \sim \text{Bernoulli}(\pi/4)\), we can compute the variance. The indicator has variance \(\text{Var}(I) = \frac{\pi}{4}(1 - \frac{\pi}{4}) = \frac{\pi(4-\pi)}{16}\), which gives our estimator variance: \[\text{Var}(\hat{\pi}_N) = 16 \cdot \frac{\text{Var}(I)}{N} = \frac{\pi(4-\pi)}{N}\]
The standard error is therefore \(\text{SE}(\hat{\pi}_N) = \sqrt{\frac{\pi(4-\pi)}{N}} \approx \frac{1.64}{\sqrt{N}}\).
The standard error decreases as \(O(1/\sqrt{N})\), which is the typical Monte Carlo convergence rate. To gain one decimal place of accuracy, we need approximately 100 times more samples.
By the Central Limit Theorem, for large \(N\) we have the asymptotic distribution: \[\sqrt{N}(\hat{\pi}_N - \pi) \xrightarrow{d} \mathcal{N}(0, \pi(4-\pi))\]
This provides approximate confidence intervals: \[\hat{\pi}_N \pm z_{\alpha/2} \sqrt{\frac{\pi(4-\pi)}{N}}\]
This example demonstrates the fundamental Monte Carlo approach: reformulate a deterministic problem (computing \(\pi\)) as the expectation of a random variable, then estimate that expectation using sample averages.